SVG⌗

SVG steht für “scalable vector graphics”. SVG ist eine alternative Methode, um Bilder zu speichern. Anders als zum Beispiel PNG und JPEG nutzt SVG aber keine Raster (Pixel), sondern es speichert alle Elemente des Bildes als mathematische Objekte im Koordinatensystem der Viewbox (des Canvas). Das hat den Vorteil, dass Bilder nicht “Verpixelt” werden, denn wenn man zoomt, werden die Vektoren der Objekte multipliziert. Das Bild bleibt also immer scharf.

Es gibt verschiedene Objekte. Einmal die geometrischen Formen wie Kreise oder Rechtecke. Diese haben wenige Punkte, die berechnet werden müssen. Ein Kreis zum Beispiel braucht nur den Mittelpunkt und den Radius. Auch ein Rechteck braucht nur 2 Eckpunkte (abgesehen von Farbe, Randstärke, Randfarbe, Name, Gruppe und der Ebene). Dann gibt es noch die “paths”. Das sind meist Bézier-Kurven. Diese kann man in jede beliebige Form bringen, aber sie brauchen dementsprechend mehr Punkte, die gespeichert und berechnet werden müssen. Wobei die Bézier-Kurve schon einen äußerst minimalen Ansatz wählt.

Bézier-Kurven⌗

Eine Bézier-Kurve hat mehrere Eigenschaften. Die Farbe, die Linienstärke, der Anfangs- und der Endpunkt, die Ankerpunkte und die Griffpunkte der Tangenten (Sowie Name, Ebene und Gruppe).

Eine Bézier-Kurve verbindet dabei 2 Punkte mit einer Linie (P1 und P2). Auf dieser Linie ist ein weiterer Punkt (A). Dieser Punkt auf der Linie hat einen Wert (nennen wir ihn “t”), der wie eine Prozentangabe der zurückgelegten Strecke auf der Linie ist. Also bei 0 ist er bei P1 und wenn t = 1 dann ist P bei P2. Die Bewegung von A wird dabei mit einer Linie nachvollzogen. So entsteht eine Bézier-Kurve. Dabei gibt es Bézier-Kurven verschiedenen Grades.

Wenn eine Kurve also einen weiteren Ankerpunkt hat (P3), dann ist das eine quadratische Bézier-Kurve. Um aus den drei Punkten die Kurve zu bekommen verbindet man die Punkte wieder miteinander (P1 & P2 sowie P2 & P3) und setzt jeweils wieder einen Punkt auf die Linie. Hierbei ist es entscheidend, dass beide Punkte (A1 & A2) auf der Linie mit dem gleichen t-Wert platziert sind. Dann verbindet man die beiden Punkte (A1 & A2) wieder miteinander und setzt A3 auf die Linie. A3 hat wieder den gleichen t-Wert. Wenn man dann von t = 0 bis t = 1 geht und die Bewegung von A3 nachvollzieht, ist das die Form der quadratischen Bézier-Kurve. Natürlich geht das auch mit noch mehr Punkten, man muss diese Schritte einfach immer wiederholen (diese Methode der Berechnung ist der De Casteljau Algorythmus).

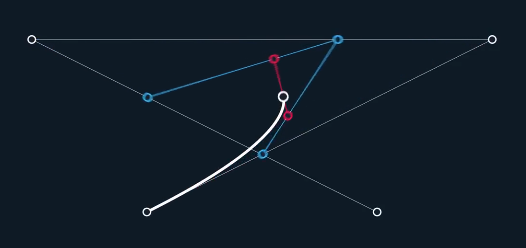
Zur eigentlichen Berechnung der Bézier-Kurven am PC wird allerdings eine andere Strategie verwendet. Dabei spielt die Entfernung des Punkts, der verfolgt wird, zu den Ankerpunkten im Verhältnis zu t eine Rolle. Durch Addieren der Vektoren kann man mathematisch schneller (aber weniger anschaulich) den Verlauf der Kurve nachvollziehen.

Hier dargestellt ist die Nähe der Kurve zu den Punkten in einer kubischen Bézier-Kurve (3-Grades)

Die Ableitung des Gleichungssystems, dass die Punkte und ihre Beziehungen zueinander darstellen, ist immer auch eine Bézier-Kurve, allerdings eine Kurve des nächst niedrigeren Grades. Das ist relevant, da man so die “Geschwindigkeit” und das Lot dazu herausfinden kann. So kann sichergestellt werden, dass die Stärke der Kurve auch immer richtig ist. Denn sonst wäre es nicht möglich, die “Bewegungsrichtung” des Punktes nachzuvollziehen, nur die Koordinaten. Dann wüsste man nicht, wo “seitlich” und wo “vorne” ist.

Ein Problem der Bézier-Kurven ist, dass es nicht möglich ist, die exakte Länge der Kurve zu berechnen (es sind nur Annäherungen möglich).

Nutzen⌗

Besonders nützlich ist SVG beim Entwerfen von Webseiten, da man sich keine Gedanken um die Auflösung machen muss und SVGs sklierbar sind.

Außerdem ist SVG in einem XML-Format gespeichert. Das kann man also in das HTML der Seite einbauen, ohne es wie bei anderen Bildern extern verlinken zu müssen. Das Bearbeiten geht aber noch weiter. Man kann SVGs auch mit dem CSS der Seite manipulieren und sogar animieren.

Zum Beispiel kann man die Farbe als Variable definieren und dann die Farbe des SVGs im CSS ändern. Und da alle einzelnen Objekte einzelne Elemente auf der Seite sind, kann man sie auch unabhängig voneinander ansprechen.

Auch beim Auswerten von Daten kommt SVG zum Einsatz, da so Punkte genau an gegeben werden können (nicht nur pixelweise).

Bearbeiten⌗

Man kann Bézier-Kurven natürlich von Hand schreiben, da sie ja XML Datein sind, aber ein GUI eignet sich schon besser. Mein Favorit ist Inkscape, da es cross plattfrom und FOSS ist.

Tangenten⌗

Beim Bearbeiten werden häufig diese Tangenten angegeben, an denen man die Kurve verändern kann. Diese Tangenten sind meistens die Verbindungen zweier Punkte. Wenn es 4 Punkte sind, dann bilden P1 & P2 die ersten Tangente und P3 & P4 die am Ende der Kurve. Da es die Punkte sind, die modifiziert werden, hat man so vollen Einfluss auf die Kurve.

Hier kann man auch die Umrahmung der Kurve sehen, die durch die Extrema (also der Ableitung) berechnet. Das ist besonders bei Kollisionsberechnungen wie zum Beispiel bei Spielen wichtig, denn der Rahmen lässt sich leichter berechnen als die genaue Position der Kurve (noch ein Grund, warum die Ableitungen von Bézier-Kurven wichtig sind).

52posts⌗

Dieser Beitrag ist Teil meines Plans, in 2023 jede Woche einen Post zu erstellen, mit Dingen, die ich gelernt habe. (Das sind dann 52 Posts).

#52posts