Physik_Q1.2
Inhalt
Klausur Schwerpunkte⌗
-
Verhältnisbestimmung bei variablen Parametern
- Konstante Spannung / Konstante Ladung
-
“halbe” Dielektriken
-
Kondensatoren in Stromkreisen
“Formelsammlung”⌗
$$ E = \frac {U}{d} \newline F_{el} = E \times q \newline I = \frac {\Delta Q}{\Delta t} \newline W = Q \times U \newline \frac{F}{Q} = \frac{U}{d} \newline W_{el} = \frac{1}{2} \times C \times U^{2} \newline W_{pot} = qEx \newline $$
elektrische Stromstärke⌗
$$ I= \frac{\Delta Q}{\Delta t} \newline Q = It $$
Die Stromstärke ist die Menge an Ladung, die in einer gegebenen Zeit fließt. Ein Ampere ist ein Coulomb pro Sekunde.
Feldstärke⌗
Die Potentielle Energie eines geladenen Körpers (mit der Ladung q) im Abstande x zur negativen Platte:
$$ W_{pot} = qEx $$
Im homogenen Feld des Plattenkondensators gilt für das Potential für jeden Punkt mit dem Abstand x zur Platte:
$$ \varphi = \frac{W_{pot}}{q} = E \times x $$
Herleitung⌗
$$ U = \Delta \varphi = \varphi \space (weil \space \varphi 1 = 0) \newline U = \frac{W{pot}}{q} \newline U =Ed \newline E = \frac{U}{d} $$
Bewegung von Teilchen im Längsfeld⌗
“Freier Fall”⌗
In diesem Fall ist das Teilchen an der Patte, die die gleiche Ladung wie es selbst trägt.
Wenn das Teilchen den Kondensator komplett durchläuft, dann gilt:
$$ W_{kin} = W_{el} \newline \frac{1}{2} \times m \times v = q \times E \times d \newline \frac{1}{2} \times m \times v = q \times U \newline v = \sqrt{\frac{q \times U \times 2}{m}} $$
“Senkrechter Wurf nach unten”⌗
In diesem Fall wird das Teilchen mit einer Anfangsgeschwindigkeit in Feldrichtung eingeschossen und weiter beschleunigt.
Bewegungsgleichungen⌗
$$ s(t) = \frac{1}{2} \times v \times t + v_0 \times t \newline s(t) = \frac{1}{2}at^{2}+v_0t \newline s(t) = \frac{1}{2} \times (\frac{q}{m} \times \frac{U}{d}) \times t^{2} +v_0t $$$$ v(t) = at+v_0 \newline a(t) = a \space (konstant) $$
Energieansatz⌗
$$ W_{kin,0} + W_{pot} = W_{kin} \newline \frac{1}{2}mv_0+qU = \frac{1}{2}mv^{2} \newline v = \sqrt{\frac{2(\frac{1}{2}mv_0^{2}+qU}{m}} $$
“Senkrechter Wurf nach oben”⌗
Das negativ geladene Teilchen wird gegen die Feldrichtung mit einer Anfangsgeschwindigkeit eingeschossen und wird abgebremst.
Da man das Teilchen voll abbremst, entzieht man ihm alle Energie. Daher gilt hier der Energieansatz:
$$ d_0 = “Bremsweg” $$$$ W_{kin} = W_{el} \newline \frac{1}{2}mv_0^{2} = F_{el} \times d_0 \newline \frac{1}{2}mv_0^{2} = qEd_0 \newline \frac{1}{2}mv_0^{2} = q \frac{U}{d}d_0 | \times \frac{d}{q \times U}\newline d_0 = \frac{1}{2} \times \frac{mv_0^{2}d}{qU} $$
Die Bewegung des Teilchens ist vergleichbar mit dem Senkrechten Wurf nach oben, da die Feldkraft hier eine ähnliche Wirkung hat, wie die Schwerkraft beim Senkrechten Wurf nach oben.
Bewegung im Längs- und Querfeld⌗
Braunsche Röhre⌗
Die Heizspannung sorgt dafür, dass in einem evakuierten Glaskolben ein Draht (Glühdraht) zum glühen gebracht wird, sodass er Elektronen aussendet.
Es liegt eine Beschleunigungsspannung U an, die die Elektronen von der Glühkatode hin zur Anode (positiv) beschleunigt.
Hinweiß: Der negativ geladene Wehnelt-Zylinder umgibt die Glühkatode, um die Elektronen zu bündeln (auf ein Loch in der Anode zu fokussieren).
$$ W_{el} = W_{kin} \newline v = \sqrt{\frac{2eU}{m_e}} $$
wenn
$$ v_0 = 0 \newline U_b = “nicht\space zu \space groß” \newline m_e = “Elektronenmasse” \newline e = “Elementarladung” \newline v = “Geschwindigkeit \space des\space Elektrons” $$
Kapazität (beim Plattenkondensator)⌗
Unter der Kapazität eines Kondensators versteht man den Quotienten aus der Ladung und der angelegten Spannung. Die Kapazität gibt also an, wie viel Ladung der Kondensator bei einer bestimmten Spannung speichern kann.
$$ C = \frac{Q}{U} $$$$ C \sim \frac{1}{d} $$$$ C \sim A $$$$ C = \Epsilon _0 \times \Epsilon _r \times \frac{A}{d} $$
Die Kapazität wird in Farad angegeben.
$$ 1 F = \frac{C}{V} = \frac{As}{V} $$
Dielektrikum⌗
Ein Dielektrikum ist ein Isolator. Als Dielektrikum können nur nichtleitende Stoffe verwendet werden, da die Ladung anderenfalls abfließen würde.
Nutzen:
-
man kann höhere Spannungen anlegen
-
die Kapazität wird gesteigert
Im Vakuum ist die relative Dielektrizitätszahl 1. Alle anderen Stoffe haben eine größere relative Dielektrizitätszahl.
Einheitenbetrachtung der elektrischen Feldkonstante:
$$ \Epsilon _0 = \frac{C}{Vm} = \frac{As}{Vm} $$
Konstante Ladung / Konstante Spannung⌗
Veränderung der Werte wenn ein Dielektrikum in den Kondensator geschoben wird.
-
Kapazität C
-
Die Kapazität erhöht sich
-
$$ C = \Epsilon _0 \times \Epsilon _r \times \frac{A}{d} = \Epsilon _r \times C_0 $$
-
-
Ladung Q
-
Bei angeschlossener Spannungsquelle (U=konstant)
-
Erhöhung der Ladung
-
$$ C > C_0 \newline C_0 = \frac{Q_0}{U} = Q_0 = C_0U \newline Q = \frac{A}{d}U \newline Q = \Epsilon _r \times Q_0 $$
-
-
Bei abgetrennter Spannungsquelle (Q=konstant)
- Q ist konstant lol
-
-
Spannung U
-
Bei angeschlossener Spannungsquelle (U=konstant)
- U ist konstant ._.
-
Bei abgetrennter Spannungsquelle (Q=konstant)
-
Verringerung der Spannung
-
$$ C = \frac{Q}{U} \newline U = \frac{Q_0}{C} = \frac{Q_0}{\Epsilon _r \times C_0} = \frac{U_0}{\Epsilon _r} \newline
$$
-
$$ C > C_0 \newline “also” \newline U < U_0 $$
-
-
-
Feldstärke E
-
Bei angeschlossener Spannungsquelle (U=konstant)
-
Feldstärke bleibt konstant
-
$$ E = \frac{U}{d}=\frac{U_0}{d}=E_0 $$
-
-
Bei abgetrennter Spannungsquelle (Q=konstant)
-
Verringerung von E
-
$$ E = \frac{U_0}{\Epsilon _r \times d} = \frac{E}{\Epsilon _r} \newline E < E_0 \newline \Epsilon _r > 1 $$
-
$$ “wenn” \newline U < U_0 $$
-
-
Energie im Plattenkondensator⌗
$$ W = \frac{1}{2} \times \frac{Q^{2}}{C} = \frac{1}{2} QU = \frac{1}{2} CU^{2} $$
Herleitung⌗
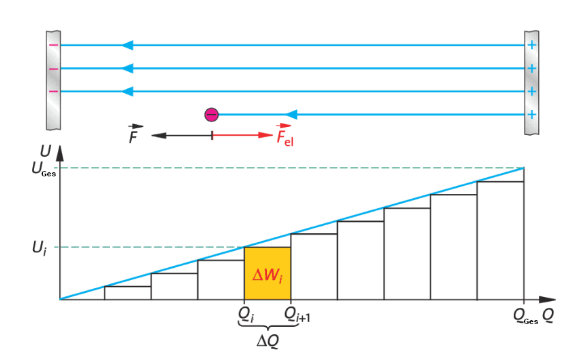
Integralrechnung⌗
$$ W_{el} = \int _{0}^{Q}U \space dq = \int _{0}^{Q} \frac{q}{C}\space dq = \frac{1}{C} \int _{0}^{Q}q \space dq = \frac{1}{2}\frac{Q^{2}}{C} $$
“Streifenmethode”⌗
$$ W_{ges} = \lim _{\Delta Q \to 0} \sum \Delta W_i = \lim _{\Delta Q \to 0} \sum \Delta Q \frac{Q_i}{C} $$
Kondensatoren im Stromkreis⌗
Parallelschaltungen⌗
$$
U_{ges} = U_1 + U_2 + U_n \newline
Q_{ges} = Q_1 + Q_2 + Q_n \newline
C_{ges} = \frac{Q_{ges}}{U_{ges}} \newline
C_{ges} = C_1 + C_2 + C_n \newline
(\frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_n} )
$$
-
Die Ersatzkapazität von parallel geschalteten Kondensatoren ist die Summe der Einzelkapazitäten
-
Durch das Parallelschalten von Kondensatoren steigt die Gesamtkapazität. Dies ist beim Plattenkondensator besonders verständlich, da die Plattenfläche, auf der sich die Ladungen ansammeln können, vergrößert.
Reihenschaltungen⌗
$$ U_{ges} = U_1 + U_2 + U_n \newline Q_{ges} = “konst.” = Q_1 + Q_2 + Q_n \newline C_{ges} = \frac{Q_{ges}}{U_{ges}} \newline C_{ges} = \frac{Q_{ges}}{U_1 + U_2 + U_n} \space | ()^{-1} \newline \frac{1}{C_{ges}} = \frac{U_1 + U_2 + U_n}{Q_{ges}} \newline \frac{1}{C_{ges}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_n} \newline (R_{ges} = R_1 + R_2 + R_n) $$
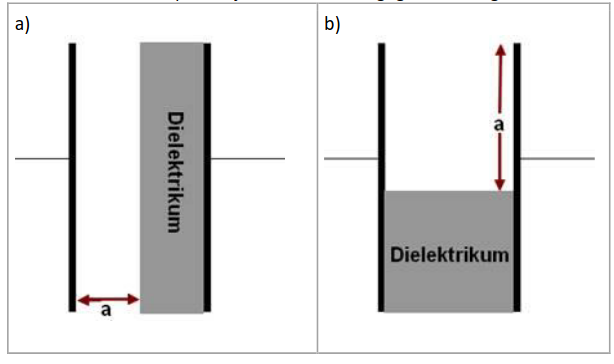
“Halbe” Dielektriken⌗
Wenn der Plattenkondensator nicht vollständig vom Dielektrikum gefüllt ist, dann teilt man den Plattenkondensator in mehrere Kondensatoren auf, um die Gesamtkapazität zu berechnen.
-
Fall a)
- Man betrachtet die zwei Ersatzkondensatoren, als ob sie in Reihe geschaltet wären
-
Fall b)
-
Man betrachtet die zwei Ersatzkondensatoren, als ob sie parallel geschaltet wären
-
$$ d = “Plattenabstand” \newline c = “Höhe \space und \space Breite, \space des \space Ursprungskondensators” \newline C_1 = \Epsilon _0 \frac{ca}{d} \newline C_2 = \Epsilon r \Epsilon 0 \frac{(c-a)c}{d} \newline C{ges} = C_1 + C_2 \newline C{ges} = \Epsilon _0 \frac{ca}{d} + \Epsilon _r \Epsilon 0 \frac{(c-a)c}{d} \newline C{ges} = \frac{\Epsilon _0 ac + \Epsilon _r \Epsilon _0 (c^{2}-ac)} {d} $$
-
Bestimmung der Elementarladung (Millikanversuch)⌗
-
geladenes Öltröpfchen im Plattenkondensator durch die Regulierung der anliegenden Spannung zum schweben bringen
-
Den Radius des Tropfens bestimmen
-
Die Fallgeschwindigkeit bei ausgeschaltetem Kondensator messen und dem Luftwiederstand die Größe bestimmen
-
Menge an Elementarladungen auf dem Tropfen bestimmen
-
Im Graphen ein Muster erkennen
-
$$ e = 1,602176634 \times 10^{-19}C $$
Kirchhoffsche Regeln und Potenziale⌗
-
Die Summe aller Ströme, die zu einem Verzweigungspunkt (einem “Knoten”) in einem Stromkreis hineinfließen, ist gleich der Summe aller Ströme, die von diesem Knoten wegfließen (Knotenregel)
-
Beim Durchlaufen einer geschlossen Schleife (einer “Masche”) eines Stromkreises ist die Summe aller Spannungen gleich null (Maschenregel)
Allgemeines⌗
Bewegungsgleichungen⌗
$$ s(t) = \frac{1}{2} \times a \times t^{2} \newline v(t) = \dot{s}(t) = a \times t \newline a(t) = \dot{v}(t) = \ddot{s}(t) = a $$